by R. Peter Broughton and R.A. Rosenfeld

INTRODUCTION AND HISTORICAL BACKGROUND

There is no shortage of sources on the historic role of the transits in determining the distance from the Sun to the Earth (which is now called the astronomical unit, or AU) and its related measure, the solar parallax, defined as the Earth's equatorial radius/AU, whose modern value is about 8.794" (arc-seconds). A comprehensive bibliography, including references to Canadian articles not cited here, can be found at:
http://www.phys.uu.nl/~vgent/venus/venustransitbib.htm.

The first recorded appearance of Venus on the Sun occurred in 1639 and it was observed by only two people, Jeremiah Horrox and his friend William Crabtree, near Liverpool, England. Horrox did attempt to use his observations to calculate the distance to the Sun, but his method had nothing to do with parallax. James Gregory was apparently the first to suggest, in 1663 (translation), that the Earth-Sun distance could be found using the parallax of Venus as seen during transits. Edmond Halley, however, is usually credited with the method, since he developed it mathematically in 1691. The parallax of the Sun can be calculated from the shift in the position of Venus as seen from locations on the Earth as far apart as possible. Since Venus appears to cross the Sun at a known rate on parallel chords bb¹ and aa¹ (Figure 1) as seen from locations B and A on Earth, and since the angular radius of the Sun is known (or can be measured), the angular distance between the chords bb¹ and aa¹ can be easily deduced from the difference between the duration of the transit as seen by two observers. Since the relative distances of Venus and Earth from the Sun are known from Kepler's third law, similar triangles, and the known distance between A and B can be used to find the actual distance gp on the Sun. So with gp known both in angular and linear measure, it is a straightforward matter to find the distance from the Earth to the Sun. While this is an oversimplified explanation, it is sufficient for understanding which measurements were required, and why. In order to make the separation gp appear as large as possible, A and B should be widely separated. For this reason, astronomers often had to travel great distances to remote sites. Their efforts were early examples of international co-operation (and to some extent, competition) on scientific missions.

When Halley first published his proposal in 1691, he did not understand the regression of the nodes of Venus' orbit well enough to make accurate long-term predictions (the "regression of nodes" is a westward drift of the orbital nodes caused by the gravitational influence of other bodies). Halley correctly recognized that the next three transits would occur in 1761, 1769 and 1874, but he missed the transit of 1882, and anticipated the next pair by eight years, giving 1996 and 2004, rather than 2004 and 2012.

ACCURACY OF THE OBSERVED TIMES OF CONTACT

There have been only four transits of Venus observed in Canada—those of 1761, 1769, 1882, 2004—and only eight sets of observations from the first three which were used in parallax determinations. They are listed in Table 1.

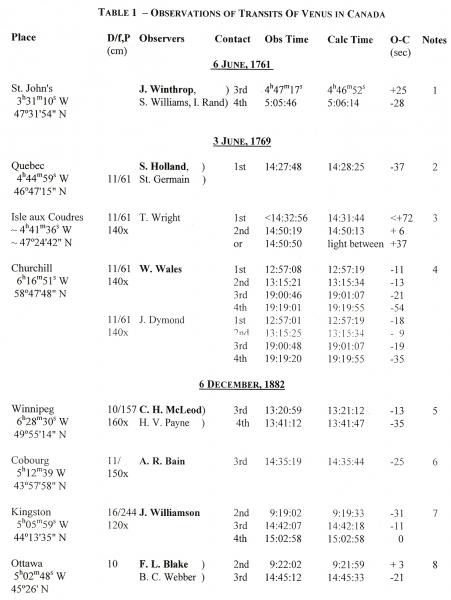
The longitude and latitude of each place are taken from modern topographic maps. The telescope used in each case is described by three numbers: D, the diameter in cm; f, the focal length in cm; and P, the magnifying power. All the eighteenth-century observers used Gregorian reflectors except Samuel Holland, who used an achromatic refractor by Dolland. The "professional" nineteenth century observers all used refractors (some amateurs employed reflectors). The principal observer at each location is listed first in boldface type. The contacts are numbered 1 (external ingress), 2 (internal ingress), 3 (internal egress), and 4 (external egress). The observed times are local apparent time for the eighteenth-century transits, and local mean time for the 1882 transit. Using topocentric apparent right ascension and declination produced by an online ephemeris generator, the calculated times of contact have been found when the separation of the centres of the Sun and Venus are equal to the sum and difference of their angular radii. The difference between the observed and calculated times is shown in seconds. In interpreting the accuracy of the observations, it should be borne in mind that the duration of the transit (between second and third contact) was the figure that was used in comparison with the duration at other sites to calculate the parallax by Halleian method (named after Edmond Halley). As an aside, it is remarkable that the duration was in error by only 8 seconds as timed by both Dymond and Wales. Observations of only one contact were sufficient for the rival Delislean method (named after Halley's friend the astronomer Joseph-Nicolas Delisle), but it required the longitude to be known with greater accuracy.